5. Sınıf 1. Tema: Çemberlerle Üçgen Oluşturma

“Çemberlerle Üçgen Oluşturma” içeriği, 2024 Ortaokul Matematik Öğretim Programı’na uygun olarak hazırlanmıştır. Aydınoloji ©

MAT.5.3.7. Matematiksel araç ve teknoloji yardımıyla düzlemde iki noktada kesişen çember çiftinin merkezleri ve kesişim noktalarından biri ile inşa edilen üçgenlerin kenar özelliklerine yönelik muhakeme yapabilme
a) İki noktada kesişen çember çiftinin merkezleri ve kesişim noktalarından biri ile inşa edilebilecek üçgenlerin kenar özelliklerine yönelik varsayımlarda bulunur.
b) Örnek çizimler üzerinden, kesişen iki çemberin merkezleri ve kesişim noktalarından biri ile inşa edilen çeşitkenar, ikizkenar ve eşkenar üçgenleri belirler.
c) Belirlediği üçgenlerin özelliklerini varsayımları ile karşılaştırır.
ç) Varsayımlarını, inşa ettiği üçgenler ile karşılaştırarak doğrulayabileceği önermeler şeklinde ifade eder.
d) Sunduğu önermelerin katkısını değerlendirir.
e) Çemberin özelliklerini kullanarak önermelerini doğrulamaya yönelik matematiksel gerekçeler sunar.
f) Çemberin özelliklerinin benzer inşa süreçlerindeki rolünü değerlendirir.

“Çemberlerle Üçgen Oluşturma” konusunu öğrenirsem ne kazanacağım? Günlük yaşamıma faydası olacak mı?

Bu konuyu öğrenmek, günlük yaşamında dünyayı daha farklı bir gözle görmeni sağlayacak. Bir mimarın binaları tasarlarken veya bir mühendisin bir köprü inşa ederken geometrik prensipleri nasıl kullandığını daha iyi anlayacaksın. Sanat eserlerinde, logolarda, hatta doğadaki bitki ve hayvan desenlerinde gizli olan matematiksel oranları ve simetrileri fark etmeye başlayacaksın. Bu da sana sadece bir ders konusu olarak değil, aynı zamanda düşünme becerilerini geliştiren, problem çözme yeteneğini artıran ve yaratıcılığını besleyen bir bakış açısı kazandıracak.

Geometri Dünyasına Hoş Geldiniz!

Bu bölümde, etrafımızdaki şekillerin sırlarını çözmeye başlayacağız! Özellikle üçgenlerin nasıl oluştuğunu ve çemberlerin bu konuda bize nasıl yardımcı olduğunu keşfedeceğiz.

Çemberleri Tanıyalım

Çemberler hayatımızın birçok yerinde karşımıza çıkar. Bisiklet tekerlekleri, saatler, madeni paralar, yüzükler… Hepsi birer çember şeklindedir. Peki, bir çemberin temel özellikleri nelerdir?

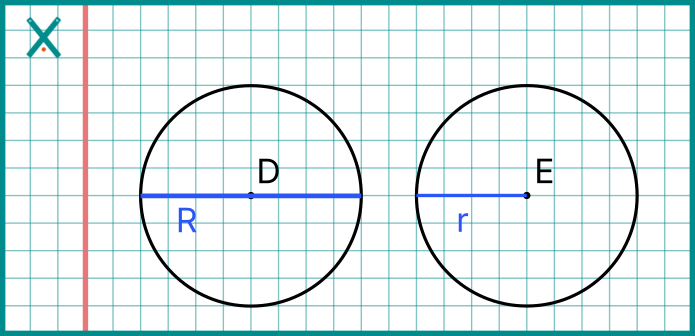
• Merkez: Çemberin tam ortasındaki noktadır. Çember üzerindeki her nokta, merkeze eşit uzaklıktadır.
• Yarıçap: Çemberin merkezinden çember üzerindeki herhangi bir noktaya olan uzaklıktır.
• Çap: Çemberin merkezinden geçen ve çember üzerindeki iki noktayı birleştiren doğru parçasıdır. Çap, iki yarıçap uzunluğundadır.

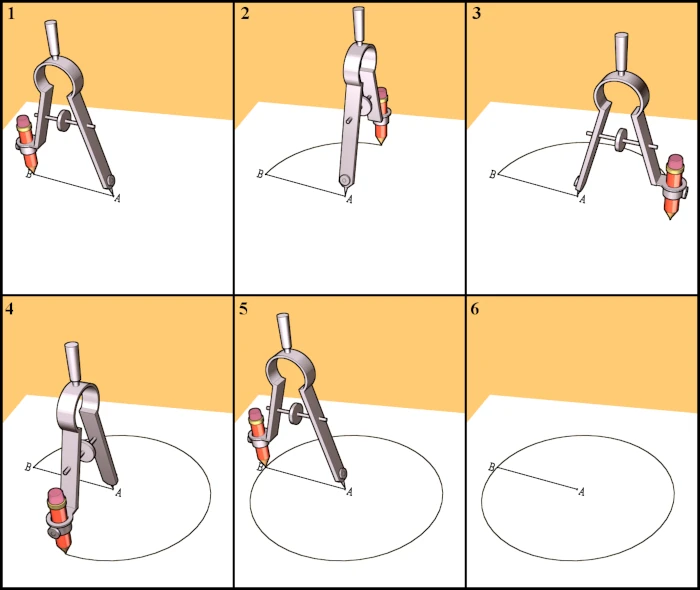
Etkinlik: Çember Çiziyoruz!

Bir pergel ve bir cetvel kullanarak farklı büyüklüklerde çemberler çizelim.

• Pergelimizin sivri ucunu kağıdın bir noktasına batıralım. Bu nokta, çemberimizin merkezi olacak.
• Pergelimizin açıklığını istediğimiz kadar ayarlayalım. Bu açıklık, çemberimizin yarıçapı olacak.
• Pergelimizi döndürerek bir çember çizelim.

Düşünelim: Aynı merkezden farklı yarıçaplarda çemberler çizersek ne olur? Ya da aynı yarıçapta farklı merkezlerden çemberler çizersek ne olur?

Kesişen Çemberler ve Gizemli Noktalar

Şimdi iki çemberi bir araya getirip iki çemberin birbirine değdiği veya iç içe geçtiği durumları inceleyeceğiz.

İki Noktada Kesişen Çemberler

İki çember, iki farklı noktada kesişebilir. Tıpkı olimpiyat halkaları gibi! Bu kesişim noktaları ve çemberlerin merkezleri bize yeni ve ilginç şekiller oluşturma fırsatı sunar: Üçgenler!

Aklımızda Bulunsun: İki çemberin kesişebilmesi için ne gibi şartlar olması gerekir? Örneğin, yarıçapları çok küçük olan iki çember çok uzakta kesişebilir mi? Hayır! Merkezleri arasındaki uzaklık, yarıçaplarının toplamından az olmalıdır.

Günlük Hayattan Örnekler:

Olimpiyat Halkaları: Dünyanın beş kıtasını simgeleyen iç içe geçmiş çemberler.

Yaşam Çiçeği: Kadim bir sembol olan ve iç içe geçmiş birçok çemberden oluşan bir desen. Bu desenler sadece güzel görünmekle kalmaz, aynı zamanda matematiksel oranları da barındırır.

Logolar ve Süslemeler: Birçok markanın logosunda veya süsleme sanatlarında kesişen çemberleri görebiliriz. Bir bankanın logosu veya bir halının deseni.

Çemberlerden Üçgen Oluşturma Sanatı

Şimdi asıl konumuza geliyoruz! İki noktada kesişen çemberlerin merkezlerini ve bu kesişim noktalarından birini kullanarak nasıl üçgenler oluşturabileceğimizi öğreneceğiz.

Matematiksel Araçlarımızı Hazırlayalım

• Pergel: Çember çizmek için kullanacağız.
• Cetvel: Noktaları birleştirip kenar oluşturmak için kullanacağız.
• Matematik Yazılımı (İsteğe Bağlı): Bilgisayar veya tablet üzerinde çalışan GeoGebra gibi bir yazılım, çemberleri dinamik olarak çizip üçgenlerin nasıl değiştiğini görmemizi sağlar.

Adım Adım Üçgen İnşası

1. İki Çember Çizin: Farklı merkezlerden, ister aynı yarıçapta ister farklı yarıçaplarda iki çember çizin. Öyle ki bu çemberler iki noktada kesişsin.
2. Merkezleri İşaretleyin: Çemberlerin merkezlerini belirleyin ve birer harf verin (örneğin B ve C).
3. Kesişim Noktasını İşaretleyin: İki çemberin kesiştiği iki noktadan birini seçin ve ona da bir harf verin (örneğin A).
4. Üçgeni Oluşturun: Şimdi A, B ve C noktalarını cetvel yardımıyla birleştirin.

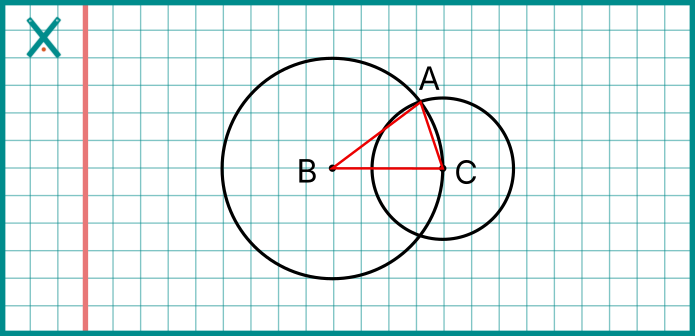
Varsayımlarda Bulunalım

Sence bu üçgenin kenarları arasında nasıl bir ilişki olabilir?

• Hepsi birbirinden farklı uzunlukta mı olacak?
• İkisi aynı uzunlukta, biri farklı mı olacak?
• Hepsi birbirine eşit uzunlukta mı olacak?

Daha fazla üçgen inşa ederek bu varsayımlarımızı test edeceğiz.

Üçgenlerin Kenar Özellikleri: Çeşitkenar, İkizkenar, Eşkenar

Üçgenleri kenar uzunluklarına göre üç farklı gruba ayırırız:

Çeşitkenar Üçgen: Tüm kenar uzunlukları birbirinden farklı olan üçgenlerdir.

İkizkenar Üçgen: İki kenar uzunluğu birbirine eşit olan üçgenlerdir.

Eşkenar Üçgen: Tüm kenar uzunlukları birbirine eşit olan üçgenlerdir.

Kendi Üçgenlerimizi İnceleyelim

Yukarıda öğrendiğimiz üçgen inşa etme yöntemini kullanarak farklı şekillerde çemberler çizelim ve oluşan üçgenlerin kenar özelliklerini inceleyelim.

Örnek Çizim 1: Çeşitkenar Üçgen İnşa Edelim

1. Bir merkezden 2 cm yarıçaplı bir çember çizin ve B harfini verin.
2. İkinci merkezi ilk merkezin 2 cm uzağına yerleştirin ve C harfini verin.
3. İkinci merkezden 1,5 cm yarıçaplı bir çember çizin.
4. İki çemberin kesişim noktalarından birini seçin A harfini verin.
5. A, B ve C noktalarını birleştirerek üçgeni oluşturun.

Bu üçgenin kenar uzunluklarını ölçtüğümüzde her kenar birbirinden farklı olacaktır. İşte bu bir çeşitkenar üçgendir.

Eğer çemberlerin yarıçapları farklıysa ve merkezler arası uzaklık da bu yarıçaplardan farklıysa, genellikle çeşitkenar üçgen oluşur.

Etkinlik

Aşağıdaki oyunda sonsuz sayıda üçgen oluşturup üçgenin verilmeyen tek iç açısını hesaplayabilirsin. Unutma! Üçgenlerde iç açıların toplamı daima 180 derecedir.

Örnek Çizim 2: İkizkenar Üçgen İnşa Edelim

1. Bir merkezden 6 cm yarıçaplı bir çember çizin (C).
2. İkinci merkezi (B) ilk merkezin 8 cm uzağına yerleştirin.
3. İkinci merkezden (B) yine 6 cm yarıçaplı (ilk çemberle aynı yarıçapta) bir çember çizin.
4. İki çemberin kesişim noktalarından birini (A) seçin.
5. Çemberleri birleştirdiği varsayılan hayali çizgi üzerinden B ve C çemberleri üzerinden birer nokta seçin.
6. Noktaları birleştirerek üçgeni oluşturun.

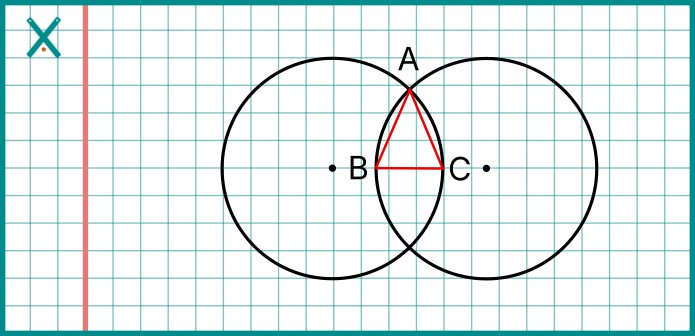
Neden İkizkenar Oldu?

• AC kenarı: B merkezli çemberin bir kirişidir.
• AB kenarı: C merkezli çemberin aynı uzunlukta kirişidir.
• BC kenarı: Çemberlerin kenarlarından seçilen noktalar arası uzaklık.

Örnek Çizim 3: Eşkenar Üçgen İnşa Edelim

1. Bir merkezden (B) 5 cm yarıçaplı bir çember çizin.
2. İkinci merkezi (C), ilk çemberin yarıçapı kadar uzağa, yani 5 cm uzağa yerleştirin. (Bu nokta, ilk çemberin üzerinde olacaktır.)
3. İkinci merkezden (B) yine 5 cm yarıçaplı bir çember çizin.
4. İki çemberin kesişim noktalarından birini (A) seçin.
5. A, B ve C noktalarını birleştirerek üçgeni oluşturun.

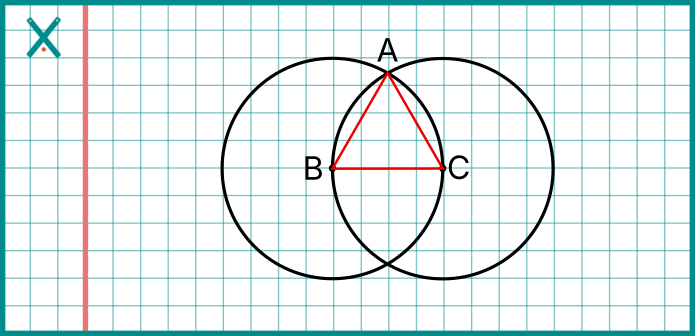
Bu üçgenin tüm kenar uzunluklarını ölçtüğünde, hepsinin 5 cm olduğunu göreceksin.

Neden Eşkenar Oldu?

• AC kenarı: C merkezli çemberin yarıçapı.
• AB kenarı: B merkezli çemberin yarıçapı.
• BC kenarı: Çemberlerin merkezleri arası uzaklık.

Bu durumda, B merkezli çemberin yarıçapı, C merkezli çemberin yarıçapı ve iki merkezin arasındaki uzaklık birbirine eşit ve yarıçap kadardır. Bu da tüm kenarların eşit olmasını sağlar ve eşkenar üçgeni oluşturur.

Bu Yöntem Neden İşe Yarıyor? (Matematiksel Gerekçe)

Bu kuralların geçerli olmasının nedeni çemberin tanımıdır. Bir çember üzerindeki her nokta, merkeze eşit uzaklıktadır. Oluşturduğumuz üçgenin kenarları, çemberlerin yarıçapları ve merkezler arası mesafeden oluştuğu için, bu uzunlukları kontrol ederek istediğimiz üçgeni bilinçli bir şekilde inşa edebiliriz.

Etkinlik

Aşağıdaki oyunda kesişen çemberleri kullanarak en kısa sürede en çok üçgeni oluşturmayı başarmalısın.

Tarihsel Bağlantı: Öklid’in “Elemanlar” Kitabı

Bu yöntem yeni değildir. Yaklaşık 2300 yıl önce yaşamış olan matematikçi Öklid, ünlü “Elemanlar” kitabının ilk önermesinde tam olarak bunu tarif etmiştir: “Verilen bir doğru parçasının üzerine bir eşkenar üçgen inşa etmek.” Bizim kullandığımız yöntem, Öklid’in bu temel geometrik ispatının pratik bir uygulamasıdır.

Ayrıca bu yöntem sadece üçgenler için değil; kare, beşgen, altıgen gibi birçok farklı çokgenin inşasında da kullanılabilir.

Geometrinin Türkçeleşmesi ve Atatürk’ün Rolü

Türkiye Cumhuriyeti’nin kurucusu Mustafa Kemal Atatürk, bilimin halk tarafından anlaşılmasını sağlamak amacıyla matematik ve geometri terimlerinin Türkçeleştirilmesine büyük önem vermiştir. 1937’de yazdığı “Geometri” kitabı ile Arapça ve Farsça kökenli birçok terimi günümüzde kullandığımız Türkçe karşılıkları ile değiştirmiştir.

Örnekler:

• Müselles → Üçgen
• Zaviye → Açı
• Dılı’ → Kenar
• Murabba → Kare
• Daire → Çember

Atatürk’ün bu çalışması, geometrinin daha kolay öğrenilmesini ve bilimin Türkiye’de yaygınlaşmasını sağlamıştır.

Bilim Sözü:

“Matematik düzen, simetri ve limitleri ortaya koyar ve bunlar güzelliğin en muhteşem formlarıdır.” – Aristotles

İçerik Sürümü: 1.0
Son Güncelleme: 15 Haziran 2025

Kaynakça

Aşağıda belirtilenler dışında; 3D çizimler, kaplama tasarımları, yapay zeka çalışmaları, sesler, mixing, mastering, animasyon, senaryo ve kodlama: aydınoloji

Akademik Kaynakça

Ortaokul Matematik Öğretim Programı (2024) T.C. Milli Eğitim Bakanlığı. 2024 Müfredatı

Euclid & Heath, T. L. (Translator/Editor). (1956). The Thirteen Books of Euclid’s Elements. Dover Publications.

Hartshorne, R. (2000). Geometry: Euclid and Beyond. Springer.

Coxeter, H. S. M., & Greitzer, S. L. (1967). Geometry Revisited. The Mathematical Association of America.

Kiselev, A. P. (2006). Kiselev’s Geometry, Book I: Planimetry. Sumizdat.

Boyer, C. B., & Merzbach, U. C. (2011). A History of Mathematics. Wiley.

Stillwell, J. (2010). Mathematics and Its History. Springer.

Görsel Kaynakça

Mcgill at English Wikibooks, Public domain, via Wikimedia Commons

Euclid, Public domain, via Wikimedia Commons

Kullanılan Yapay Zeka Sistemleri

Dil Denetimi: AU-GPT 4.5

Kod Üretim Desteği: https://chatgpt.com

Psikolojik Denetim: AU-GPT 4.5