“Çokgenler” içeriği, 2024 Ortaokul Matematik Öğretim Programı’na uygun olarak hazırlanmıştır. Aydınoloji ©
MAT.5.3.5. Çokgenleri düzlemde ardışık olarak kesişen doğruların oluşturduğu kapalı şekiller olarak yorumlayabilme
a) Düzlemde en az üç doğrunun son doğru ilk doğruyla kesişecek biçimde ardışık kesişerek oluşturdukları durumları inceler.
b) Düzlemde en az üç doğrunun son doğru ilk doğruyla kesişecek biçimde ardışık kesişimleri ile çeşitli çokgenler oluşturur.
c) Çokgenlerin düzlemde en az üç doğrunun son doğru ilk doğruyla kesişecek biçimde ardışık kesişimleri ile meydana geldiğini ifade eder.
MAT.5.3.6. Çokgenlerin özellikleri ile ilgili edindiği deneyimleri yansıtabilme
a) Çokgenlerin özellikleri ile ilgili edindiği deneyimleri gözden geçirir.
b) Çokgenlerin kenar ve açı özelliklerine dair çıkarım yapar.
c) Çıkarımını farklı örnekler üzerinden değerlendirir.
“Çokgenler” konusunu öğrenirsem ne kazanacağım? Günlük yaşamıma faydası olacak mı?
Bu içeriği okuduğunda Çokgenler konusunu öğreneceksin. Çokgenleri öğrenmek, çevrendeki dünyayı daha iyi anlamana yardımcı olur. Çünkü binalar, yol tabelaları, halı desenleri, karo döşemeleri gibi günlük hayatta sıkça karşılaştığın pek çok nesne aslında çokgenlerden oluşur. Bu konuyu öğrendiğinde; şekilleri tanımlayabilir, düzgünlüklerini anlayabilir, ölçümler yapabilir ve kendi tasarımlarında geometrik düzeni estetikle birleştirebilirsin. Ayrıca problem çözme, dikkat ve akıl yürütme becerilerin de gelişir.
Doğrularla Şekil Oluşturma
Eline bir cetvel al ve boş bir kâğıda en az üç doğru çiz. Bu doğruların birbirini sırayla kestiğini ve en sonunda son doğrunun ilk doğruyla birleştiğini düşün. Ortaya ne çıkar? Eğer bu doğrular birbirine bağlanıp kapalı bir şekil oluşturuyorsa, buna “çokgen” denir.
Çokgen nedir?
- En az üç doğru parçasının ardışık olarak kesişmesiyle oluşan kapalı şekillerdir.
- Son doğru, ilk doğruyla kesişmelidir.
İlk Çokgenlerimizi Tanıyalım
Bazı özel çokgenleri tanıyalım:
3 doğru → Üçgen
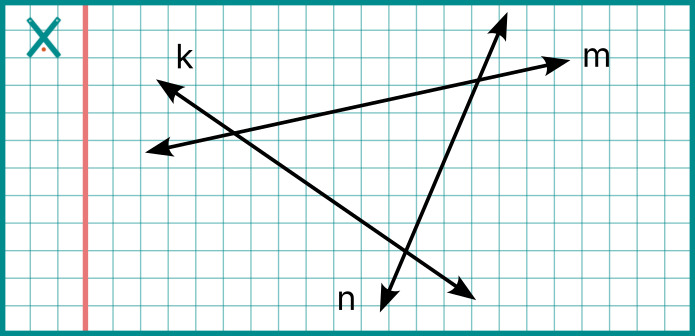
4 doğru → Dörtgen

5 doğru → Beşgen

6 doğru → Altıgen
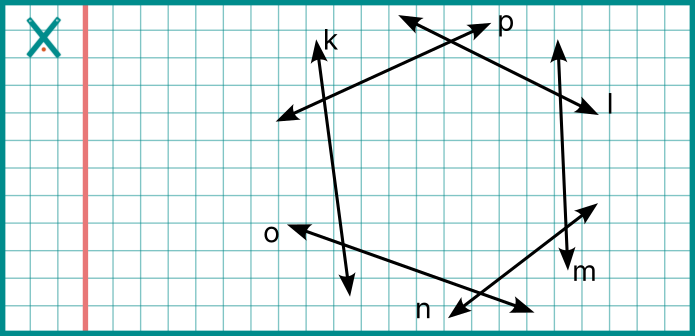
Bu şekillerde doğruların nasıl birleştiğini ve kapalı şekiller oluşturduğunu gözlemleyerek, şeklin adı belirlenir.
Çokgenlerin Temel Elemanları
Her çokgenin 3 önemli özelliği vardır:
Köşe: İki doğrunun birleştiği nokta.
Kenar: İki köşe arasındaki doğru parçası.
Açı: İki kenarın birleştiği noktada oluşan aralık.
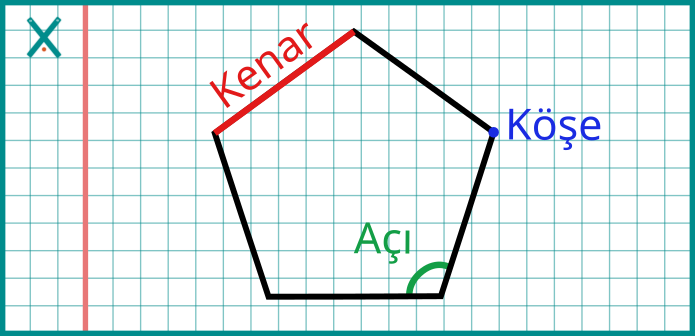
Bir üçgende 3 köşe, 3 kenar, 3 açı; bir dörtgende 4’er tane bulunur.
Oyun: Şekil Fabrikası
Çokgenlerin Adlandırılması
Çokgenlerin adını verirken köşeleri kullanırız. Örneğin:
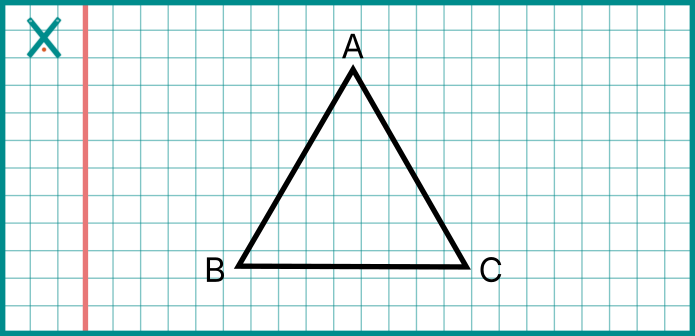
A, B ve C noktaları bir üçgenin köşeleriyse → ABC Üçgeni denir.
D, E, F, G noktaları bir dörtgenin köşeleriyse → DEFG Dörtgeni denir.
Köşeler sıralı olarak okunmalıdır.
İç Açı ve Dış Açı
İç açı: Çokgenin iç bölgesinde kalan açıdır.
Dış açı: Komşu bütünler açı olan, dış bölgede kalan açıdır.
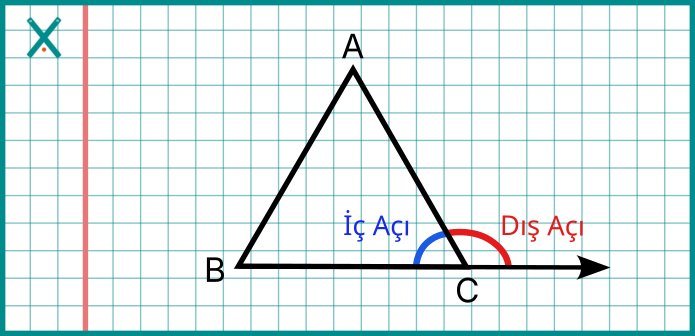
Bir çokgendeki köşe sayısı kadar iç ve dış açı vardır. Dörtgenin dört köşesi varsa, dört iç ve dört dış açısı olur.
(Etkinlik: Öğrenciler bir çokgenin iç ve dış açılarını cetvel ve açıölçer yardımıyla belirlemeye çalışır.)
Düzgün Çokgenler
Düzgün çokgen:
- Tüm kenar uzunlukları eşittir.
- Tüm iç açı ölçüleri eşittir.
Örnekler:
- Eşkenar üçgen (her kenar eşit)
- Kare (her kenar ve açı eşit)

Biliyor muydun?
Arılar en verimli bal saklama yöntemi olduğu için altıgen petekler üretir ve bunların için balla doldururlar:

Ölçme Etkinlikleriyle Çokgenleri İnceleme
Çizilen çokgenlerde:
- Her kenar cetvelle ölçülür.
- Her açı açıölçerle ölçülür.
Düzgünlük kontrolü:
Yukarıdaki eşkenar üçken görselini dikkatlice inceleyin:
- Tüm kenarlar eşit mi?
- Tüm iç açılar eşit mi?
Çokgen İnceleme Oyunu
Aşağıdaki oyunu oynayarak çokgenlerle ilgili çok sayıda soru üretip yanıtlayabilirsin.
Köşegen Nedir?
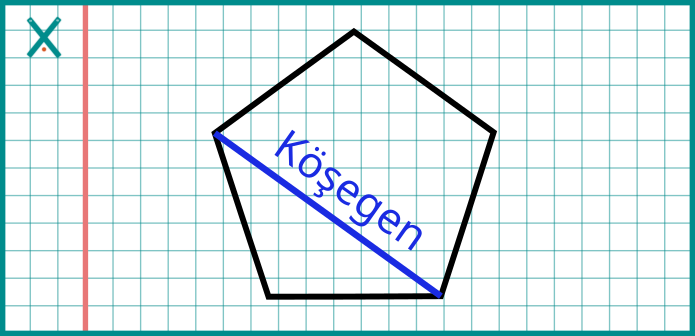
Köşegen: Bir çokgende ardışık olmayan iki köşeyi birleştiren doğru parçasıdır.
- Üçgende köşegen yoktur.
- Dörtgende 2 köşegen vardır.
- Beşgen, altıgen gibi daha büyük çokgenlerde daha fazla köşegen bulunur.
Üçgenlerde Açılar ve Üçgenin İç Açıları Toplamı
Üçgenlerde ne kadar çok şekil görsek de önemli bir kural vardır:
- Üçgenin iç açıları toplamı daima 180 derecedir.
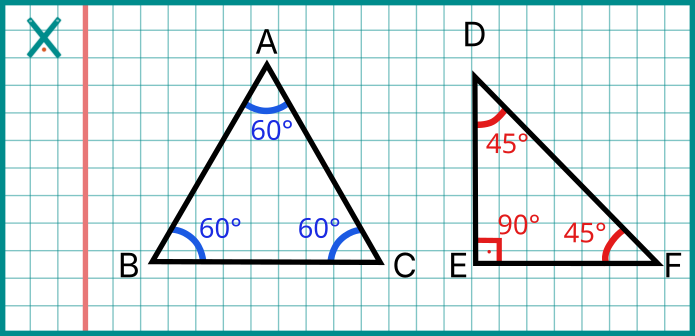
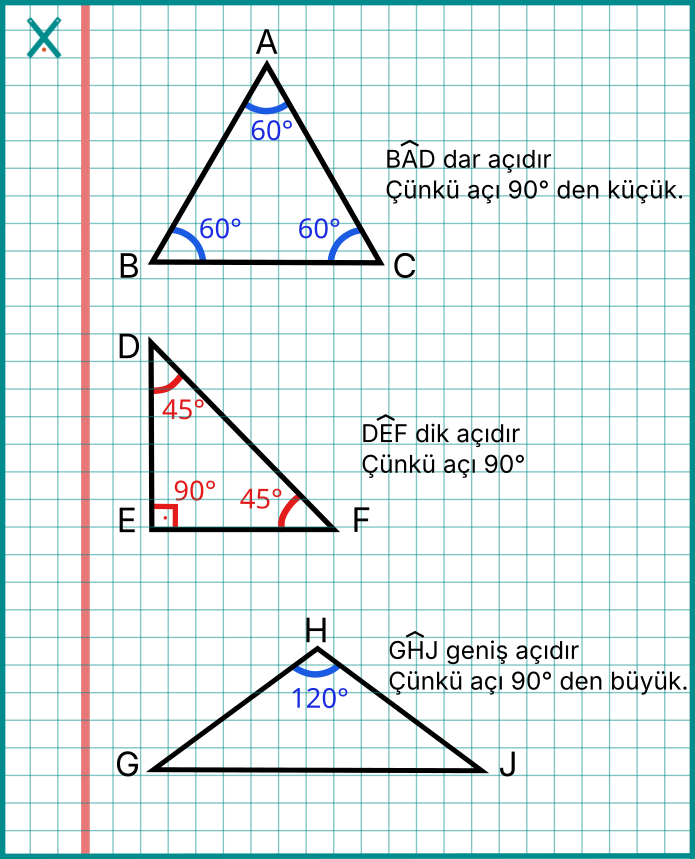
Açı çeşitleri:
- Dar açı: 90 dereceden küçük
- Dik açı: 90 derece
- Geniş açı: 90 dereceden büyük
Üçgen çeşitleri (açılara göre):
- Dar açılı üçgen
- Dik açılı üçgen
- Geniş açılı üçgen
Üçgen Türleri ve Kavram Haritası
Kenarlarına göre üçgenler:
Eşkenar Üçgen: Tüm kenarlar eşit

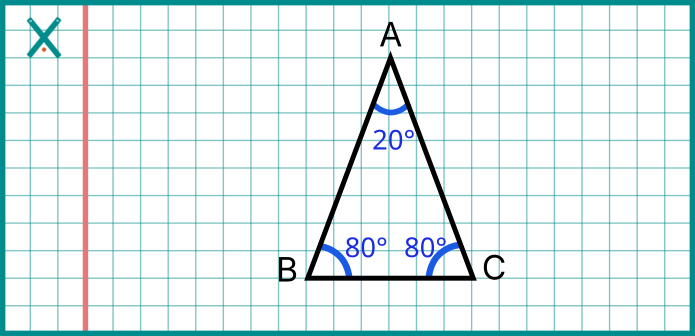
İkizkenar Üçgen: İki kenar eşit
Çeşitkenar Üçgen: Bütün kenarlar farklı

Bilim Sözü:
"Matematik düzen, simetri ve limitleri ortaya koyar ve bunlar güzelliğin en muhteşem formlarıdır." - Aristotles
İçerik Sürümü: 1.0
Son Güncelleme: 15 Haziran 2025
Kaynakça
Akademik Kaynakça
Ortaokul Matematik Öğretim Programı (2024) T.C. Milli Eğitim Bakanlığı. 2024 Müfredatı
Van de Walle, J. A., Karp, K. S., & Bay-Williams, J. M. (2019). Elementary and Middle School Mathematics: Teaching Developmentally (10th ed.). Pearson.
Common Core State Standards Initiative – Geometry (Grade 5).
http://www.corestandards.org/Math/Content/5/G
NCTM (National Council of Teachers of Mathematics). Principles and Standards for School Mathematics.
Jones, K. (2002). Issues in the Teaching and Learning of Geometry. In: Aspects of Teaching Secondary Mathematics, edited by Linda Haggarty.
Görsel Kaynakça
Fotoğraf: Pixabay: https://www.pexels.com/tr-tr/fotograf/bal-koyan-arilarin-ustten-gorunumu-56876/
Kullanılan Yapay Zeka Sistemleri
Dil Denetimi: AU-GPT 4.5
Kod Üretim Desteği: https://chatgpt.com
Psikolojik Denetim: AU-GPT 4.5
Bir yanıt yazın