8. Sınıf 5. Ünite: Basit Makineler

“Destek ve Hareket Sistemi” içeriği, 2018 Fen Bilimleri Öğretim Programı’na uygun olarak hazırlanmıştır. Aydınoloji ©

2. Bölüm: Destek ve Hareket Sistemi
F.8.5.1.1. Basit makinelerin sağladığı avantajları örnekler üzerinden açıklar.
a. Basit makinelerden, sabit makara, hareketli makara, palanga, kaldıraç, eğik düzlem ve çıkrık üze rinde durulur.
b. Dişli çarklar, vida ve kasnakların da birer basit makine olduğu görsellerle belirtilir, ayrıntıya girilmez.
c. Basit makinelerde işten kazanç olmadığı vurgulanır.
ç. Matematiksel bağıntılara girilmez.
F.8.5.1.2. Basit makinelerden yararlanarak günlük yaşamda iş kolaylığı sağlayacak bir düzenek tasarlar.

“Basit Makineler” konusunu öğrenirsem ne kazanacağım? Günlük yaşamıma faydası olacak mı?

Bu içeriği okduğunda “Basit Makineler” konusunda anlamadığın noktaları öğreneceksin. Basit makineleri bilmek, günlük hayatta iş yapmayı kolaylaştırır ve fiziksel kuvveti daha verimli kullanmayı sağlar. Örneğin, bir kaldıraçla ağır bir nesneyi kaldırmak daha az kuvvet gerektirirken, eğik bir düzlem kullanarak bir yükü yukarı taşımak daha az enerji harcamanızı sağlar. Bu bilgiler, evde tamir işlerinden profesyonel makine kullanımlarına kadar birçok alanda pratik çözümler üretmenize yardımcı olur. Böylece hem zamandan hem de fiziksel çabadan tasarruf edilir.

Basit Makineler Nedir?

Basit makineler, iş yapmayı kolaylaştıran araçlardır. Genellikle az sayıda parçadan oluşurlar. Örneğin, bir kaldıraç ya da makara birer basit makinedir.

Basit makinelerin özellikleri:

• Kuvvetin büyüklüğünü ve yönünü değiştirebilir.
• İş veya enerjiden kazanç sağlanamaz, ancak kuvvetten ya da zamandan ya da yoldan kazanç sağlanabilir.
• Kuvvet kazancı varsa, yoldan kayıp vardır.
• Yol kazancı varsa, kuvvetten kayıp vardır.
• Kuvveti farklı enerji türlerine dönüştürebilir.

Kuvvet Kazancı Nedir?

Kuvvet kazancı, bir basit makinenin uygulanan kuvveti ne kadar artırdığını ifade eder. Eğer basit makineye uygulanan kuvvet, basit makineden elde edilen kuvvetten küçükse kuvvet kazancı var demektir.

Örnek: 100 Newton ağırlığındaki bir cismi, 50 Newton kuvvet uygulayarak kaldırıyorsanız kuvvet kazancı 2 kat olmuş demektir.

Unutmayın: Kuvvet kazancı 1’den büyükse, kuvvetten kazanç sağlanır; 1’den küçükse kuvvetten kayıp olur. Eğer kuvvet kazancı 1’e eşitse kuvvetten kazanç ya da kayıp yok demektir.

Makaralar

1. Sabit Makaralar:

• Sabit bir yere asılıdır ve yalnızca kuvvetin yönünü değiştirir.
• Kuvvet kazancı = 1 ’dir. Bu nedenle kuvvetten veya yoldan kazanç sağlanmaz.
• Kullanım örneği: Bayrak direği.

2. Hareketli Makaralar:

• Makara yükle birlikte hareket eder.
• Kuvvetten kazanç sağlanır (Kuvvet kazancı = 2), ancak yoldan kayıp vardır.
• Kullanım Alanları: İnşaat vinçleri.

3. Palangalar:

• Sabit ve hareketli makaraların birlikte kullanıldığı sistemlerdir.
• Kuvvet kazancı hareketli makara sayısına bağlıdır.
• Kullanım Alanları: Liman vinçleri, asansör sistemleri.

Not: Makaralarda aynı ip üzerindeki gerilmeler eşittir.

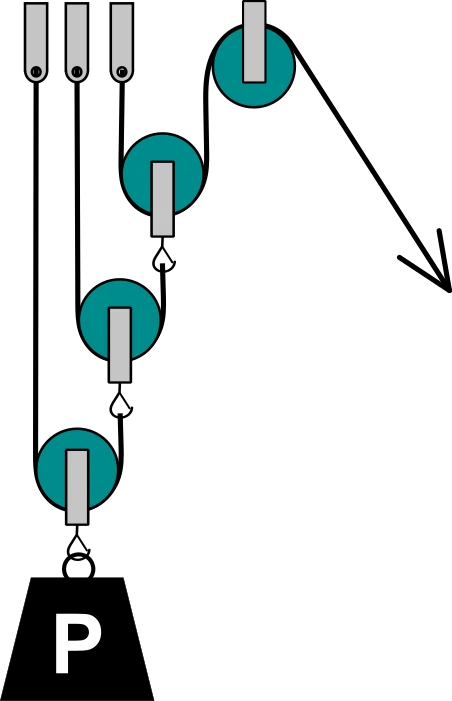
Aşağıdaki videoyu izleyerek makaraların çalışma mantığını öğrenebilirsiniz.

Kaldıraçlar

Kaldıraçlar, bir destek noktası etrafında hareket eden çubuklardır. Kuvvet ve yük kolları, kaldıraçlarda hesaplamalar için temel oluşturur.

Formül: Kuvvet x Kuvvet Kolu = Yük x Yük Kolu (Bu formül aşağıdaki üç düzenek için de geçerlidir)

Destek Ortada: Kuvvetin yönü değişir. Örnekler: Tahterevalli, makas.

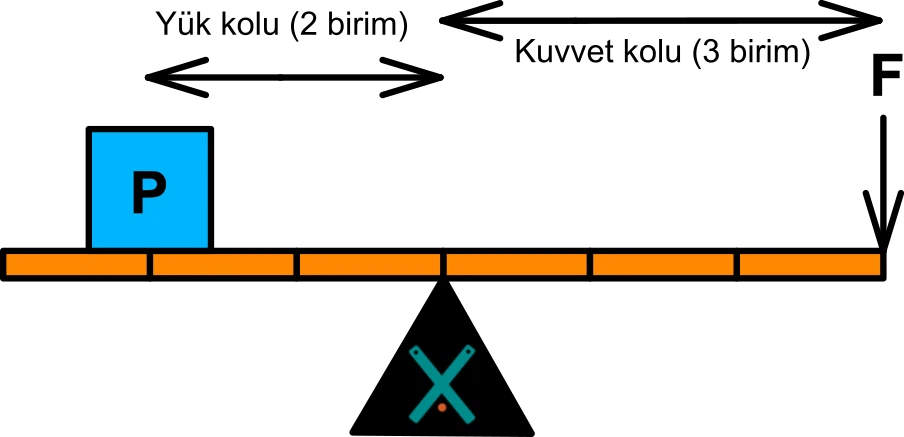
Yük Ortada: Kuvvet kazancı sağlanır. Örnekler: El arabası, ceviz kıracağı

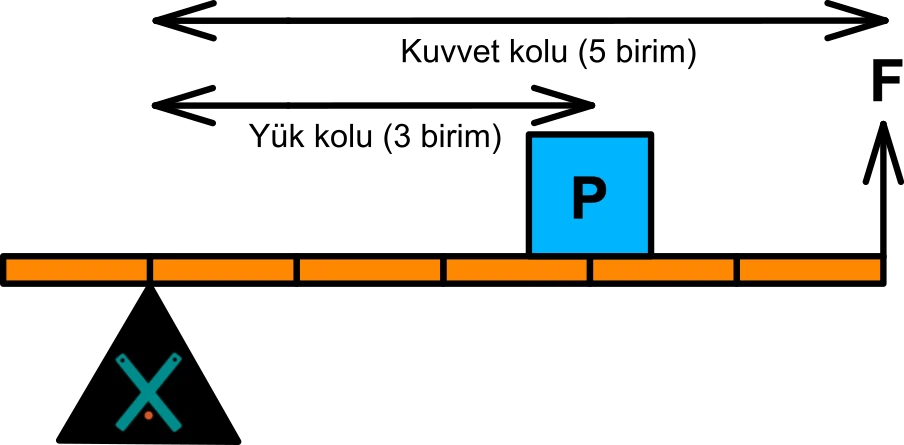
Kuvvet Ortada: Yoldan kazanç sağlanır. Örnekler: Cımbız, maşa.

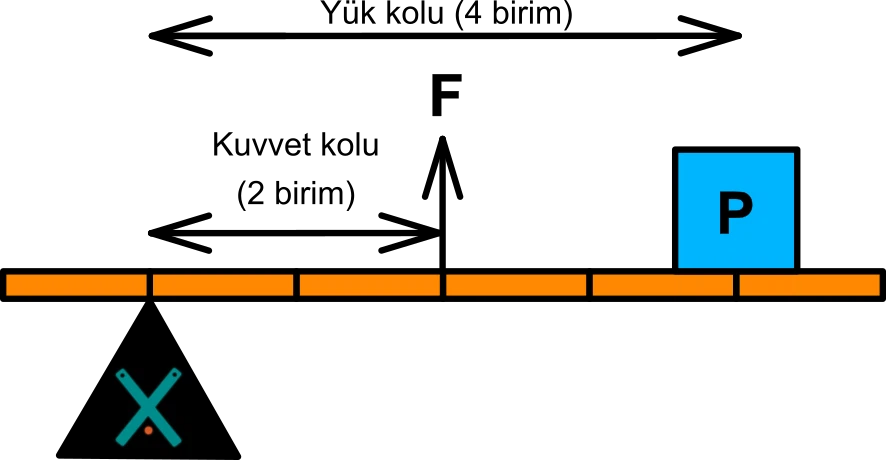
Eğik Düzlem

Ağır yükleri daha az kuvvetle yukarıya taşımak için kullanılan basit makinelerdir.

Formül: Kuvvet (F) x Yol = Yük (P) x Yükseklik

Özellikler:

• Kuvvetten kazanç vardır, ancak yoldan kayıp olur.
• Eğik düzlemin boyu uzadıkça kuvvetten kazanç artar.

Kullanım Alanları: Kaydırak, rampa, su kaydırakları, vida.

Aşağıdaki videoyu izleyerek eğik düzlemde hesaplama yapmayı ve çalışma mantığını öğrenebilirsiniz.

Biliyor muydunuz? Vida aslında silindire sarılmış bir eğik düzlemdir.

Bu konuda 3D çıktısını alabileceğiniz bir eğitim materyalimiz bulunuyor. Buraya tıklayarak indirebilirsiniz.

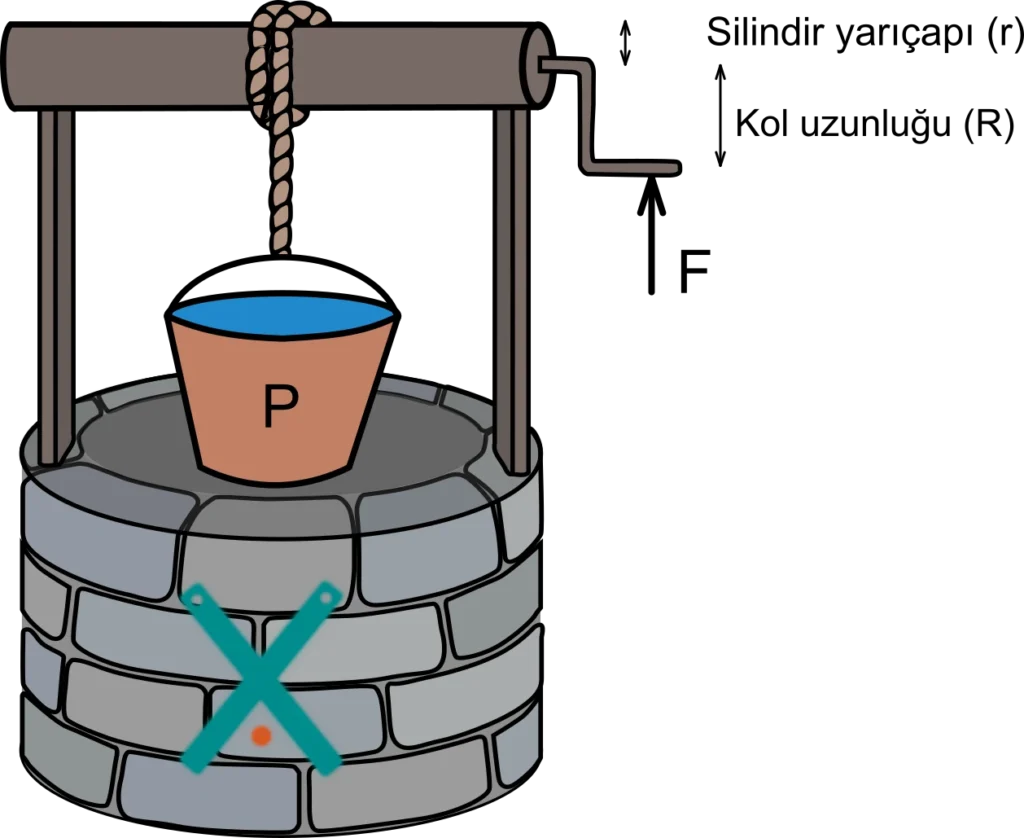
Çıkrık

Dönme eksenleri aynı olan iç içe geçmiş silindirlerden oluşur. Çıkrık, kuvvetten kazanç sağlar, ancak yoldan kayıp olur.

Formül: Kuvvet (F) x Kol uzunluğu (R) = Yük (P) x Silindir yarıçapı (r)

Kullanım Alanları: Kuyudan su çekme düzeneği, kahve değirmeni.

Diğer Basit Makineler

Dişli Çarklar: Hız ve yön değişimi sağlar.

• Kullanım Alanları: Bisiklet, saat mekanizması.

Kasnaklar: Kayışla bağlanan silindirlerdir.

• Kullanım Alanları: Motorlu araçlar, fabrika makineleri.

Vida: Silindirin etrafına sarılı eğik düzlemdir.

• Kullanım Alanları: Mobilya montajı, makine parçaları.

Tekerlek: Hareketi kolaylaştırır.

• Kullanım Alanları: Arabalar, el arabaları.

Bileşik Makineler

Birden fazla basit makinenin birleşmesiyle oluşan sistemlerdir.

Örnekler:

• Bisiklet: Dişli çark, tekerlek, çıkrık ve kaldıraç.
• El Arabası: Tekerlek, eğik düzlem ve kaldıraç.

Genel Değerlendirme

Son olarak, bu makinelerin günlük hayatımızı nasıl kolaylaştırdığını tartışalım. Kuvvet kazancı, zaman tasarrufu ve yol kazancı gibi özelliklerin nerelerde öne çıktığını inceleyelim.

Kaynakça

Akademik

Fen Bilimleri Öğretim Programı (2018) T.C. Milli Eğitim Bakanlığı.

Hewitt, Paul G. Conceptual Physics. Addison-Wesley, 2006.

Meriam, J.L., ve Kraige, L.G. Engineering Mechanics: Statics and Dynamics. John Wiley & Sons, 2007.

Georgia State University. HyperPhysics. http://hyperphysics.phy-astr.gsu.edu/hbase/Mechanics/simmac.html

Görsel

Görsel 1: Photo by Chad Kirchoff on Unsplash